《自复制自动机理论》冯·诺依曼

书的编者是冯纽曼的助手Arthur W. Burks，遗传算法之父John Holland的博士生导师。

2.2.1.1.1 图灵机

第二堂课 控制与信息理论

五、图灵机

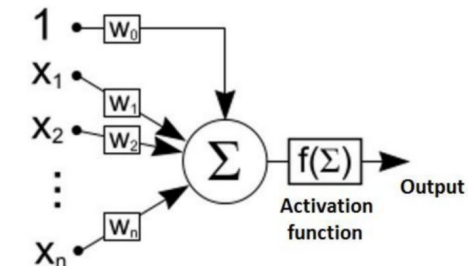
McCulloch & Pitts 自动机的基本结构是神经元，McCulloch & Pitts 得出结论，认为公理化的神经元体系同形式逻辑是等价的。

图灵关于有限自动机的结论：存在通用图灵机AU，具有以下性质：对于任何图灵机A和程序I，存在模拟程序IA，只要提供IA和I给AU，AU就可以模拟A 的运算，输出和A执行I得到的相同结果。AU 具有模拟任何图灵机去执行任何指令的能力，哪怕这个图灵机比AU 本身要复杂得多也没关系。因为通用图灵机本身的复杂性不足，可以由模拟器程序包含的内容来填补。这项研究的深刻之处在于，只要把通用图灵机恰当地制作出来，它就能够完成任意复杂的工作，因为其他的各种需求可以通过编写程序来满足。但是，只有当任意的图灵机 A 具有最起码的复杂度，从而能够实现通用图灵机的时候，它才能有这样的能力。换句话说，没有达到通用图灵机复杂度的系统，不管你给它写什么程序，都是不可能完成某些工作的。但是一旦复杂性超越了某一个确定的阈值，只要给予适当的程序，所有的自动机都能够相互模拟了。人类第一次具有了某种通用的工具，理论上说，只要任何人能够做到的事，这种工具也能复现此过程。

图灵还发现了自动机的极限。也就是说，无法制造这样一种自动机，这台自动机能够预测其他自动机在有限时间内是否能解决某个问题，完成停机。换句话说，虽然你可以制造能够模拟任何图灵机的通用图灵机，你却无法制造可以预测任何图灵机运行结果的“预测机”。做过的事情可以重复，但是没有做过的事情，却没有办法预测。