AI成为主脑科学家（AI-masterbrain Research）：AI介导的五阶段科学革命（The Five Stages of AI-involved Scientific Revolution）
LeCun：AI将带来人类的新文艺复兴，一种新的启蒙运动，因为AI将放大每个人的智力。这就像每个人都有一群比自己更聪明，对大多数话题都更加熟悉的人在帮助自己。它将赋予我们每个人更大的权力。
ChatGPT不会拥有人类的创造力，没有意识和动机，即使他学会了推理，但AI以他不断进化的能力，帮助人们拓展文明的边界，帮助人们抵达文明新的高度。物理学家大卫·布儒斯特，他在目睹了国际象棋机器人及其引起的科学探索之后，说了一句意味深长的话：“那些本来为了取悦普通人而发明出来的自动化玩具，现在正在用于开拓我们人类的能力并将文明带向更新的境界。”
Stuart Russell：目前的人工智能系统没有通用性，因为电路无法很好地捕捉通用性。我们已经在大型语言模型很难学习算术的基本规则中看到了这一点。尽管有数百万个例子，之前击败人类的人工智能围棋系统还是无法正确理解 “大龙” 和 “死活” 的概念，作为业余围棋选手的研究员开发出了一套策略，战胜了围棋程序（“20230223 绝艺”）。
《Sparks of Artificial General Intelligence: Early experiments with GPT-4》
8.2 Lack of planning in arithmetic/reasoning problems
GPT-4：7 * 4 + 8 * 8 = 88
作者用 100 个随机样本对模型进行了测试，在 0 到 9 之间均匀生成四个数字，得到的准确率只有 58%。这只涉及到个位数的乘法和两位数字的加法，一个具备基本数学知识的小学生就能解决这个问题，当数字在 10 ~ 19 之间和 20 ~ 39 之间均匀选择时，准确度分别下降到 16% 和 12%，当数字在 99 和 199 之间时，准确度下降到零。
《哥德尔、埃舍尔、巴赫：集异璧之大成 Gödel, Escher, Bach: An Eternal Golden Braid》Hofstadter
CHAPTER XIX Artificial Intelligence: Prospects
Ten Questions and Speculations
Question: Will a thinking computer be able to add fast?（智能计算机是否能更快地做加法？）
Speculation: Perhaps not. We ourselves are composed of hardware which does fancy calculations but that doesn’t mean that our symbol level, where “we” are, knows how to carry out the same fancy calculations. Let me put it this way: there’s no way that you can load numbers into your own neurons to add up your grocery bill. Luckily for you, your symbol level (i.e., you) can’t gain access to the neurons which are doing your thinking-otherwise you’d get addle-brained. To paraphrase Descartes again:
“I think; therefore I have no access to the level where I sum.” （我思，故我无法进入我算的层次）
Why should it not be the same for an intelligent program? It mustn’t be allowed to gain access to the circuits which are doing its thinking otherwise it’ll get addle-CPU’d. Quite seriously, a machine that can pass the Turing test may well add as slowly as you or I do, and for similar reasons. It will represent the number 2 not just by the two bits “10”, but as a full-fledged concept the way we do, replete with associations such as its homonyms “too” and “to”, the words “couple” and “deuce”, a host of mental images such as dots on dominos, the shape of the numeral ‘2’, the notions of alternation, evenness,
oddness, and on and on … With all this “extra baggage” to carry around, an intelligent program will become quite slothful in its adding. Of course, we could give it a ‘ pocket calculator , so to speak (or build one in). Then it could answer very fast, but its performance would be just like that of a person with a pocket calculator. There would be two separate parts to the machine: a reliable but mindless part and an intelligent but fallible part. You couldn’t rely on the composite system to be reliable, any more than a composite of person and machine is necessarily reliable. So if it’s right answers you’re after, better stick to the pocket calculator alone-don’t throw in the intelligence!
扩展一下：泛化能力/鲁棒性与出错/幻觉/胡话、原理黑箱是通用智能的一体两面（2.2.1.1.3 容错、自修复、鲁棒性）。
有些场景中，大模型的一些现有缺陷对商用的影响没那么大，甚至可能是助益。如强调个性化和趣味性的聊天应用 character.ai 创始人说：“我并不认为幻觉是需要解决的问题，我甚至很喜欢它，这是模型有趣的特点。” 在 character.ai 做的 “角色扮演” 聊天场景中，幻觉是想象力的源泉。但对另一些容错很低的行业，如医疗诊断、自动驾驶、工业自动化，幻觉却危害显著。
群集模型系统：在凯文·凯利《失控：机器、社会与经济的新生物学》一书中描述了复杂系统的进化、涌现和失控。人类大脑的神经网络、蚁群、蜂群这类系统的动作是从一大堆乱哄哄却又彼此关联的事件中产生的。从群体中涌现出来的不是一系列个体行为，而是众多个体协同完成的整体动作。AI 大模型也符合群集系统的特点。由于缺乏中心控制，群集系统效率相对低，如大模型就存在信息冗余，且不可预测、不可知、不可控。但缺乏中心控制也带来了可适应、可进化、无限性和新颖性的优势，因此大模型能通过涌现自学新技能。
06 延展大问题：如何让数学、编码和逻辑更可靠 我们尚未完全理解GPT-4的能力源于何处
赫伯特·西蒙(Herbert Simon)：“从行为系统的角度来看，人类相当简单。我们随时间表现出的行为复杂性很大程度上源于我们所处环境的复杂性。”
有时，当规模足够大时，复杂行为会从最简单的组成部分中涌现。
08 聪明的科学 从基础研究方面转化为临床实践问题
把基础生物学中的大语言模型（如Alphafold2）与大量包括生物医学知识在内的人类语言表达（如GPT-4）整合在一起。这种回报可能表现为一种全面的大语言模型——我们称之为“全知博士”(Dr.One-With-Everything)，它整合了蛋白质结构、其他基本的生物数据库（如基因调控和人类基因变异）、临床前研究以及临床试验的设计与实施。在21世纪30年代中期，这种包罗万象的模型很可能成为生物医学研究的核心智能工具。过去200年中形成的基础科学研究、药物发现、临床需求评估和临床研究等领域彼此孤立的状态将无法适用于全知博士这种广泛的概念整合者。
结语 欣赏AI的奇迹，人类智慧和无尽雄心的见证 悲伤的阶段
OpenAI对AGI的定义：“在大多数有经济价值的工作中胜过人类”。
拒绝相信大语言模型可能具有“智能”的自然冲动极为强烈：预测下一个词语是什么竟然能导致智能产生！智能一直是智人生存的主要优势，进化可能使人类物种对其赋予了极高的价值，因此，我们可能本能地认为带来智能的机制宏伟且庄严。就我个人而言，我确实天生就相信智能的架构必须具有高度复杂性和异质的结构。我相信，一定存在更高层次的符号结构，而这些结构一定是构成我们认知能力的基础。但是，也许正如我们无论如何都无法通过意志力让大脑看透一种已经被解释得很清楚的错觉一样，我们也可能被迫去相信诸如因果推理、常识推理、数学问题解决、规划、自我激励、目标设定等事务，是基于比大语言模型背后复杂的数字结构更复杂的结构实现的。GPT-4是否会迫使我们面对一个可能性，即智能产生的机制比我们曾经认为可能的情况要简单得多？
塞巴斯蒂安·布贝克的文章，对比了GPT-4对人类认知的冲击与哥白尼发现地球并非宇宙中心，以及沃森和克里克发现所有生命都是由四种碱基序列定义的相似之处。这些科学发现都挑战了我们对人在自然秩序中的地位的自负。
合作伙伴关系
作为一个社会的成员，乃至一个物种，我们需要做出一个选择。我们要想清楚我们是要因为害怕AI带来的风险和明显的危害可能性而限制甚至扼杀它？还是要屈服于AI，任由它自由取代我们，削弱我们的能力和需求？抑或是我们要从今天开始，共同塑造我们的AI未来，以期实现单凭人类或AI无法实现，而人类与AI结合却可以完成的目标，达到更高的成就？这个选择权掌握在我们手中，而且很有可能在未来不到10年的时间里就需要做出决定。
《Sparks of Artificial General Intelligence: Early experiments with GPT-4》
到底发生了什么？What is actually happening?
对 GPT-4 的研究完全是现象学的：研究者们专注于 GPT-4 可以做的令人惊讶的事情，但没有解决它为什么以及如何获得如此惊人的智能这一基本问题。它是如何推理、计划和创造的？当它的核心仅仅是简单的算法组件——梯度下降，和具有极其大量数据的大型 Transformer，为什么它表现出如此普遍而灵活的智能？ 它挑战了大家对学习和认知的理解，激发了大家的好奇心，并激发了更深入的研究，而一个关键的研究方向就是对于 LLM 涌现机制的探索。
然而，尽管人们对 LLM 的能力问题产生了浓厚的兴趣，但迄今为止的进展非常有限。一个普遍的假设是大量的数据（特别是内容的多样性）迫使神经网络学习通用的和有用的「神经环路」，而大尺寸的模型为神经环路提供了足够的冗余和多样性，以支持专业化和微调到特定的任务。为大规模模型证明这些假设仍然是一个挑战，而且，几乎可以肯定的是，猜想只是答案的一部分。从另一个角度来看，模型的巨大规模可能会带来其他一些好处，例如通过连接不同的最小值或简单地实现高维数据的平滑拟合，从而使梯度下降更加有效。总的来说，阐明 GPT-4 等人工智能系统的性质和机制是一项艰巨的挑战。
是什么让ChatGPT变得如此聪明？仍然未知的大语言模型“能力涌现”现象
当我们不断加大模型规模时，大语言模型表现出：
第一类：上下文学习ICL（In Context Learning，2022年初正式提出）。ICL的关键思想是不对模型参数进行调整，而是给大模型几个示例，AI就可以从类比中学习。论文：OpenAI《Language Models are Few-Shot Learners》https://arxiv.org/pdf/2005.14165.pdf；华盛顿大学、Meta、Allen Institute for AI《Rethinking the Role of Demonstrations: What Makes In-Context Learning Work?》https://arxiv.org/pdf/2202.12837.pdf
第二类：思维链CoT（Chain of Thought），是大语言模型推理能力的重要来源之一。论文：Google Brain团队《Chain of thought prompting elicits reasoning in large language models》https://arxiv.org/pdf/2201.11903.pdf
目前涌现仍然是黑箱，我们对能力涌现的机制与方向还所知甚少。
针对涌现最核心的论文是以下两篇：
Google+DeepMind+Stanford等《Emergent Abilities of Large Language Models》（大语言模型的涌现能力）https://openreview.net/pdf?id=yzkSU5zdwD
UCLA 3位教授《Emergent Analogical Reasoning in Large Language Models》（类比推理能力在大语言模型中的涌现）https://arxiv.org/pdf/2212.09196.pdf
OpenAI 推测，涌现也许是一种类似进化的机制。Ilya Sutskever的论文《学习生成评论并发现情感》中提到，当给了足够的模型容量、训练数据和计算时间后，GPT 大模型内部自行产生了一个情感分析功能单元，能准确辨别文字是在表达喜悦、悲伤还是愤怒。（类似于《AI3.0》“机器“观察”到的东西有时与我们截然不同”：网络学会的是将具有模糊背景的图像分到“包含动物”这一类别，无论该图像是否真的包含一只动物。）
论文认为，这有可能是因为能辨别情感色彩，对 GPT 更好完成其目标，即预测下一个词有很大帮助。就像人类为了生存繁衍这个单一目标，进化出了复杂的生理特征和文化习俗，那些更适宜生存、让种群扩大的特点会被保留，涌现可能就是这样一个类似自然选择的进化过程。而进化的另一面是失控，能进化的东西，本身不会是完全可控和可以提前设计的。进化不光创造新技能，也可能创造出幻觉。学会使用一个正在快速进化的黑箱工具，是人类以前没遇到过的课题。我们需要在接受、理解和适应失控的前提下，寻找可控的部分，避免商业风险和更大的风险。
2023冷门歌手：孙燕姿，2023热门歌手：AI孙燕姿。
关于“AI孙燕姿”，2023-05-22孙燕姿本人在她网站的blog作出回应：“我的 AI”。
中文翻译（Translation courtesy of joyapple）
当我正在为自己凸出的肚子和孩子们的日常琐事烦心时，AI孙燕姿已正式“出道”，于是我决定来写一些对它的感想。
我的粉丝们都已跳槽，也同时接受我就是一名冷门歌手的事实，而我的AI角色也成为了目前所谓的顶流。毕竟该怎么跟一个每几分钟就能推出一张新专辑的“人”比呢？
无论是ChatGPT、AI或叫什么名字都无所谓，这个“东西”能够通过处理海量的信息，同时以最连贯的方式拼接组合手头的任务，来模仿和/或创造出独特而复杂的内容。等一下，这不就是人类已经在做的吗？之前我们一直坚信，思想或观点的形成是机器无法复制的任务，这超出了它们的能力范围，但现在它却赫然耸现并将威胁到成千上万个由人类创造的工作，比如法律、医学、会计等行业，以及目前我们正在谈论的，唱歌。
你可能会反对，说自己还是能分辨，它既没有情绪，也没有音调（或任何你能想得到的专业术语）的变化。很抱歉，我怀疑这只会是个非常短暂的反应。
讽刺的是，人类再怎么快也无法超越它。没有人类能够获得如此大量的信息并且在正确的时机做出正确的决策，或者犯下正确的错误（OK，或许我想得有点太远）。这项新技术将能够为每个人提供他们所需要的一切，无论是独立的、扭曲的还是疯狂的，都可能会有一种专门为你创作的独特内容。你并不特别，你已经是可预测的，而且不幸的是，你也是可塑的。
此时此刻，我觉得自己像是一个在吃着爆米花、坐在电影院最好的位置上的观众。（顺便说一句：这种情况下，很可能没有任何技术能预测我本人是什么感受，直到这篇文章出现在网络上）。这就像看那部改变了我们生活的电影《瞬息全宇宙》，有别于电影的是，爱并不是拯救这一切的关键。
在这无边无际的汪洋大海中存在，凡事皆有可能，凡事皆无所谓，我认为思想纯净、做自己，已然足够。
河森堡关于AI的一篇微博：https://weibo.com/5992829552/MCeqg2YK5
1、“GPT并行开了12个屏幕的游戏，每个屏幕都以7倍的速度对战，这意味着AI在以近百倍的速度学习反馈”：《黑客帝国》中的学习过程变成真的了。
2、AI高水平地做了大量的重复工作，让人有时间、有能力（AI能够做的底层工作就可以固化封装）在更高层面上去探索。同时AI可以极大地提升人类的学习、创新效率（林亦以前几个月做的工作，现在只需要1周时间）。现在还看不到AI完全自主的创新能力。
“ AI不会淘汰人，只会淘汰不会使用AI的人。”
林亦用GPT玩《街霸2》的视频见：https://weibo.com/tv/show/1034:4890912753647738?from=old_pc_videoshow
生成式预训练大模型表现出了 “随模型规模增长，学会更多新技能” 的规律。这种前所未有的无师自通是大模型更强通用性的主要来源。
随着参数从 80 亿增长到 5400 亿， Google PaLM 大模型学到了多个新技能。
《AI3.0》
10游戏只是手段，通用人工智能才是目标
哈萨比斯：通用人工智能可以根据自身的经验和数据来学习如何做事。
DeepMind对于其在AlphaGo项目上取得的成果的最为重要的声明：“我们的结果全面地证明了一个纯粹的强化学习方法是完全可行的，即便在最具挑战性的领域，不用人类的示例或指导，除基本规则之外不提供任何其他领域的知识，程序也有可能训练到超人类水平。”
在机器学习领域，有一个充满前景的学习方法，那就是“迁移学习”（transfer learning），它是指一个程序将其所学的关于一项任务的知识进行迁移，以帮助其获得执行不同的相关任务的能力。人类从一种任务到另一种任务的能力迁移看起来毫不费劲，我们对所学知识进行泛化的能力正是思考的核心部分。迁移学习的本质就是学习本身。与人类形成鲜明对比的是，当今人工智能领域中的大多数学习算法在相关的任务之间是不可迁移的。
国际象棋或围棋这样的游戏可以教会人们如何更好地思考：如何进行逻辑思考、抽象推理和战略规划。这些都是能够让人受用一生的能力，也是可以在所有事情中使用的通用能力。AlphaGo并没有学会更好地“思考”除围棋之外的其他任何事情。除了围棋之外，它不具备任何思考、推理和规划的能力。它所学到的能力没有一项是通用的，也没有一项可以被迁移到任何其他任务上。
尽管AlphaGo等深度Q学习系统已经在某些细分领域上取得了超人类的表现，但是它们缺乏一些对人类智能而言非常基本的东西，比如抽象能力、“域泛化”（domain generalization）能力，以及迁移学习能力，如何使系统获得这些能力仍然是人工智能领域最重要的开放问题之一。这些系统并未以人类的方式来学习的另一个原因是：与监督学习系统一样，这些深度Q学习系统极易受到对抗样本的攻击。对输入做出某种人类无法察觉的微小改变会严重损害程序的表现。
扩展：AI需要对“通用的学习能力”进行学习（二阶学习）。现阶段AIGC方面取得了一定的通用能力泛化的进展，但还需要有一个“通用的学习能力”方法的质变的过程（类似于Transformer之与NLP）。
AutoML-GPT: Automatic Machine Learning with GPT
https://mp.weixin.qq.com/s/DGrWcoJv2AQXiL_bNM8z0Q
https://papers.labml.ai/paper/35151be0eb2011edb95839eec3084ddd
二阶神经网络的一个例子：ToT（Tree of Thoughts思维树）
Stephen Wolfram（2023/2/14） ：
《What Is ChatGPT Doing … and Why Does It Work?》
中文：《ChatGPT的工作原理》 / 《ChatGPT是在做什么……为什么它有效？What Is ChatGPT Doing … and Why Does It Work?》
详细解构了神经网络以及ChatGPT的底层机制，以及进一步探讨了ChatGPT能几乎完美的和人类对话这个事实所触及的本质：人类语言（及其背后的思维模式）在结构上恐怕比我们想象的更简单、更具有“法则性”。而ChatGPT恰巧隐式的发现了这个法则。ChatGPT只是从其积累的“常识统计”中提取出一些“连贯的文本线索”。ChatGPT的底层人工神经网络结构最终是基于对大脑的理想化建模的，能够成功地“捕捉到”人类语言及其背后的思维的本质。语言的丰富性和它所能谈论的事物可以被封装在这样一个有限的系统中。很可能当我们人类生成语言时，许多方面的情况都非常相似。ChatGPT证明了一个基本的科学事实，即大量简单的计算元素可以做出卓越而出乎意料的事情。
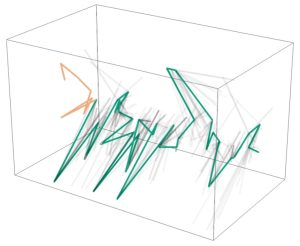词空间向量的轨迹
用GPT-4解释了GPT-2三十万个神经元 《Language models can explain neurons in language models》
LLM主要的超参数有：词表大小（Vocab_Size）、最大位置编码大小（Max_Position_embeddings）、隐层节点数大小（Hidden_Size）、隐层数（Num_Hidden_Layer）、注意力头数（Num_Attention_Heads）。
《ChatGPT 的训练过程解析》
模型+训练（PreTrain）：“人工标注数据+强化学习”（RLHF，Reinforcement Learning from Human Feedback ）。四个人工专家调优/训练的主要阶段：Pretraining 预训练、Supervised Finetuning 有监督微调、Reward Modeling奖励建模、Reinforcement Learning强化学习
莱布尼茨：“一旦人们对最大部分的概念建立起‘普遍语言’，那时人类将会拥有一种新工具，它提高智能的能力，远胜过光学工具之加强人眼。它的用途之大，从其中会进而产生出什么，这取决于命运之手，但它肯定会带来重要的和卓越的结果。”
大语言模型（Large Language Model， LLM）之所以有了突破，本质上是把语言问题转化成了数学问题。
乔治·博克斯（George Box）：“所有模型都是错的，但有一些有用（All models are wrong，but some are useful）。”
四、自复制自动机的核心
图片：http://informatics.indiana.edu/rocha/ss504_5.html
假设自动机 X的符号串（用二进制代码表示的自动机）是Φ(X)。
我们可以设计一台通用构造器（Universal constructer）A，当我们把Φ(X)喂给A的时候，它就能够逐步地利用悬浮在周围的零件，把 X 一点点的组合出来。
存在一台通用拷贝机器B(copy automaton)，当我们把任何描述输入B的时候，B 就会制造出同样的两份描述出来。
把机器A和B组合在一起，并给 A+B 添加一个控制器C。C按照下列方式对A和B施加控制：C先命令B拷贝两份描述Φ(X)；然后再命令A按照Φ(X)来实际制造X，并把其中的1份Φ(X)拷贝去掉；最后，C会把X和剩下的那份Φ(X)捆在一起，并把它们从机器A+B+C 的组合中间分离出去，这样一来，我们就制造出了 X+Φ(X)这样的组合。
我们用（A+B+C）来代替X，并进行上述同样的操作，那么(A+B+C)+Φ(A+B+C)的自动机组合，就可以制造出自动机组合：(A+B+C)+Φ(A+B+C)出来。 五、自复制自动机的进化
让X代表A+B+C+D，这里D代表任何自动机。那么(A+B+C)+Φ(A+B+C+D)就可以制造出(A+B+C+D)+Φ(A+B+C+D)。换句话说，自复制机器不仅仅有复制自己的能力，还可以顺便生产出其他的组件 D 的能力。这就是任何自复制生命都具备的功能：在复制自身的时候，它还会创造出副产品。
作为一个系统，(A+B+C+D)可以发生类似变异的过程。“变异”是指中间有一个零件发生随机的变化。如果是A、B或者 C 的一个零件发生了变化，那么系统通常就会失去自复制的能力。但是如果变异发生在描述Φ(A+B+C+D)上面，那么系统制造出的就不再是它自己，而是修改后的自己，下一代自动机能否继续复制取决于变异发生的具体位置。如果A、B 或者 C发生了变化，那子代自动机就会“绝后”。但是如果变异发生在D 的描述上，那么除了 D变成了D’之外，变异的子代同母体系统完全相同。之后的子代会把这个变异D’继承下去。这就是可遗传变异的基本过程。这套系统已经具备了可遗传变异的基本特性。大多数随机变异都是致命的，但是也可能偶尔会发生非致命乃至是可遗传的变异。
如果用X代表“身体”，Φ(X)：基因，A：子宫，B：卵巢、精囊，
则C：代表生殖系统中的调控和控制机制，如激素调节和生殖过程的精细控制。这些控制机制确保了生殖过程的正常进行，从而使得基因（Φ(X)）和身体（X）得以成功地结合和繁衍。（GPT-4）
D：新模块、新功能（逐步演化成新物种）。
关于“C”：
《未来大历史》大卫·克里斯蒂安
第3章 细胞何以管理未来？
DNA包含着信息，就像是菜谱一样，但它实际上做不了任何事。在某一时刻决定细胞行为的是此刻真正派上用场的基因组合。而被称为转录因子(transcription factor)的工作分子的活动则起决定作用。这些转录因子能感知到细胞内外的情况，它们会运用这些信息来“决定”还需要生产哪些分子或者需要把哪些新的分子丢弃。转录因子会潜入DNA当中，破解其制造相关分子的指令。然后，它就会开启分子的生产过程（或者让不再需要的蛋白质停止生产）。无论什么时候，生物的基因组中只会有某些基因得到“表达”。基因组的其他部分都被关闭或者等待被读取使用的那一刻（有时，它们得永远等下去）。在某一特定时刻决定哪些基因派上用场的过程被今天的生物学家称为表观遗传(epigenetic)过程。它们不会让基因组发生改变，但它们确实影响着特定的基因何时得以表达以及如何表达。这些非遗传性因素决定基因会在何时以何种方法派上用场。这些过程会告诉细胞此刻正在发生什么，又该为哪些情况做好准备。
在DNA双链外有许多的表观遗传活动：蛋白质和RNA分子掌握的新信息关乎迫在眉睫的威胁或是潜在的机会，用分子级的扳手和杠杆来拆解特定的DNA阶梯——要么读取该部分的遗传密码，要么让其难以发挥作用。如果需要某种新的蛋白质，某种特别的分子级转录因子就会沿着DNA双链寻找某个特定的基因。当转录因子找到这个基因时，它便会拆开几级碱基对阶梯，把螺旋阶梯的那一部分撬走。转录因子还会找来信使RNA(mRNA)。在这段已经暴露在外的基因中，RNA会读取其碱基对的字母序列并加以储存。
然后这几级被打开的阶梯又会被锁回去，而信使RNA现在带着的便是一份碱基对清单——制造蛋白质新品的配方。它会就此向着细胞质进发，并停靠在某个核糖体（各种蛋白质的集合体）面前，而RNA的作用有点像3D打印机。核糖体抓住信使RNA，读取它从DNA那儿拷贝来的氨基酸订单。然后，核糖体就会在周围抓所需的氨基酸，把它锁定在长链的某个位置上并确保顺序正确，这样某种特定的蛋白质就能制造出来了。由300个氨基酸组成的蛋白质，核糖体只需一分钟就能制造出来。
第四堂课 大数之道
三、不同的纠错模式
生物材料具有某种工程上的特别稳定特性，而这种稳定性又是同其机械、电子和可靠性要求所匹配的。而我们的人工装置则是一种“凑合”，往往为了达到电子上的指标，结构上却变得多余累赘。我们用到的技术，常常是适合把金属和金属连接在一起，却不适用于把金属和电子管连接起来。在难以触及的真空管中间达到一毫米的空间已经是一项工程上的壮举了，我们很难把这个尺度再缩小多少。因此，工程自动机和生物细胞尺度上的差距，实质上来自于材料性质上的巨大不同。
如果按照“有错必纠”的完美主义理念，像生命这样的复杂系统很难持续比几个毫秒更长的时间。生命应该是同概率完全整合在一起的，它可以在错误里面持续运行。在生命中的误差，不会像在计算过程中那样不断地扩散放大。生命是十分完善且具有适应性的系统，一旦中间发生了某种问题，系统会自动地认识到这个问题的严重程度。如果无关紧要，那么系统就会无视问题，继续运作；如果这个问题对于系统比较重要，系统就会把发生故障的区域封闭起来，绕过它，通过其他的候补渠道继续运行等等。然后在有空的时候，系统回头再去修复故障，如果不能修复，那么系统就把这个区域永久地废弃。所以，整个生物体的可靠性长度取决于要多长时间才会出现固定数量的不可修复故障，进行了多少次的调整和永久绕行，以及到最后，要多久才会彻底无计可施，再也无法修复。生命同那种一触即溃，一个错误就会土崩瓦解的系统，完全就是两回事。
第三堂课 信息的统计理论
一、自动机的鲁棒性
那些被严格程序所控制的仅仅是一些细节结构。大部分的控制是以一种允许错误，并且在错误发生时候采取补救措施（多少有效）的方式来实现的。而且，说它们能够预防失误还有些夸大，因为这种机制其实根本就不可能消除所有错误，而是实现了一种发生个别的失误根本无关紧要的容错状态。在这种机制下，无论是错误还是失误带来的后果，都不能被彻底消除。我们可以努力去做到的事情，就是设计一台自动机，让它在遇到通常错误后仍然可以照常工作。这种设计的目的是减小错误的影响，而不是去消除错误。