《复杂的引擎》The Engine Of Complexity 约翰·E.梅菲尔德
第5章 无概率性和复杂引擎
如何弥补现实极端的不可能性?
让计算的输出作为其自身(相同的规则集)的输入,这个过程我们称之为迭代(不断地重复)。如果迭代计算是确定性的,会有3种可能的结局:收敛到某个最终的输出/输入不再变化;进入循环,相同的输出/输入以规则的间隔反复出现;或者形成混沌。如果计算是概率性的,则还有第4种可能:输出可能不断随机变化。
存在一个普适性的策略,允许算法和数据都随机变化,同时还能确保循环的继续。如果迭代计算中加入了程序变化的可能性,通常会有3个特点:
·程序必须实现某种复制机制,并且这种机制要允许发生错误或其他变化。
·每次循环中的错误(变化)必须很小。
·每次循环必须有足够多的输出,这样至少有一个输出相对当前循环的输入没有显著变化。
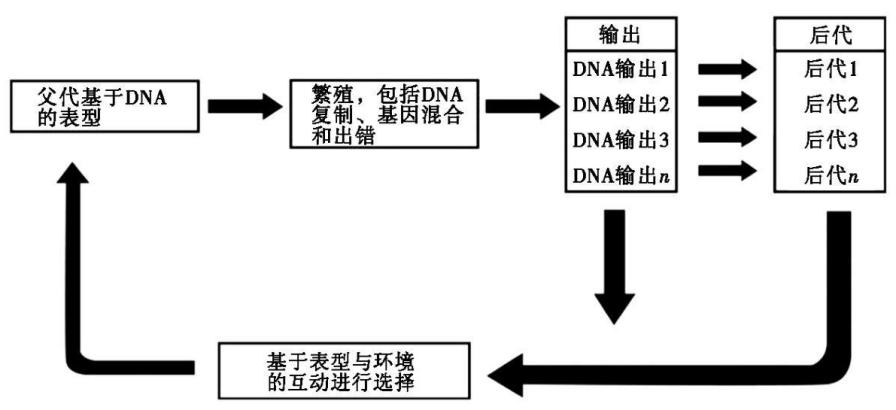
如果具备这3个特点,迭代计算就能长期进行,程序(规则和输入数据)改变但计算不会停止。由于每次循环有多个输出,所以必须有某种选择机制,因为没有哪个系统能让输入/输出的数量无限增长。我们可以将具有这些特性的通用计算策略称为“选择性迭代概率计算”(IPCS,Iterated Probabilistic Computation with Selection)。这种系统会表现出渐进式变化。图5.2绘制了其基本特性。内环是所有进化过程的定义性特征,也是我所说的复杂引擎。这个引擎就是IPCS,是有多重输入和输出的并行计算。
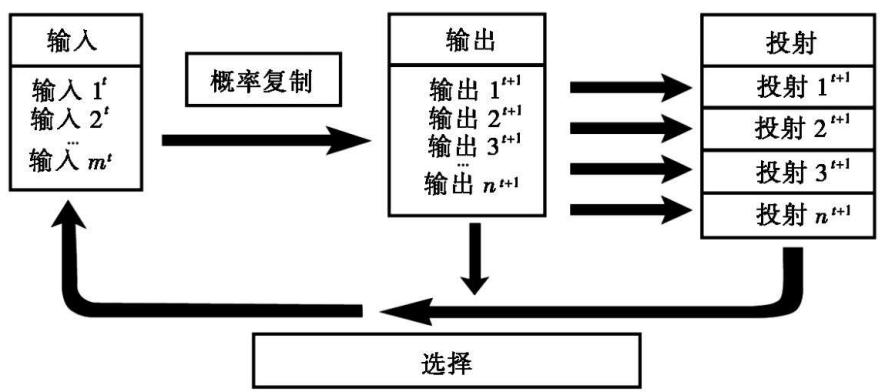
具有复杂引擎的循环系统一般都会以输入/输出结构的形式累积信息,改进的个体被再次复制的机会更高。这个循环在随机的变化中保留更符合选择标准的变化,从而提炼信息。一旦出现随机变化,就会根据选择规则对产生的输出进行评估。如果变化是好的,就会成为下一轮循环的输入,如果不好,就会被淘汰。
图5.2中标有“投射”的方框不是引擎的基本组成部分,但大部分进化系统都有这个特性。在这样的系统中,选择作用于产物,而不是直接作用于输出。对于生物,输出是DNA序列,产物是生物体。
可以非随机地选择输出作为下一轮循环的输入。本质上选择涉及产物(生物体)与环境的互动。有时候选择规则很明确,有时候又是间接的和概率性的,具有复杂引擎的系统在非随机选择规则的作用下都会逐渐演变。在改变的过程中,系统自然而然会累积符合选择规则的信息。如果施加新的选择规则,系统又会马上开始累积符合新规则的信息。新信息的来源是被选择的随机变化。产生和保留的最简单的可能变化构成了最基本的信息单元。通过反复的选择和保存记录,系统就能逐渐累积相关的信息。如果选择是非随机的,累积的信息也会是非随机的。IPCS策略的力量和美在于其能在没有预先计划的情况下表现出最大的创造性。
生命是计算的产物吗?
图5.3将生命进化描绘成了一个循环过程。选择通过成功的繁殖实现,繁殖的成功又取决于个体与环境的复杂互动。图5.3中的循环就是图5.2中的循环的特例。由于DNA编码信息,因此图5.3也描绘了计算。DNA编码的信息既是循环过程的输入也是输出。
人类学习和创造性
现在有哪些理论?
大脑也被视为神经元网络,但网络编码的是概率分布。首先,更高级别的大脑核心发展和维护关于我们所处世界的不同方面的思维模型,并用这些模型不断评估和预测。第二,预测和感知数据都编码为概率分布。这意味着数据和预测都包含对其不确定度的估计。第三,感知数据处理的主要任务是最小化不确定度,让输入的感知数据与预测相匹配。模型预测与输入感知数据之间的不匹配(不确定度)可以从两个方面减小,要么是改变感知数据(例如移动),要么是修正内部模型。修正内部模型是学习的一种形式。
如果输出是预测,不确定度反映的是预测和感知输入的不匹配,则通过调整网络权重减少不确定度就可以改进模型。因此通过将“意外”最小化,大脑就能自动调整其内部模型,使得内部预测与感知数据匹配得更紧密。高层大脑将内部模型的预测向下投射,低层大脑则计算预测与输入感知数据的不匹配(不确定度)并向上投射。
复杂引擎在大脑中可能起作用,有两个原因使得这个想法很具有吸引力:(1)以往的经验表明,只要应用得当,复杂引擎型的计算很擅长为困难的问题找到很聪明的以前从未想到过的答案;(2)这种方法与贝叶斯脑的原理相容。一旦复杂引擎的思想与贝叶斯脑相结合,有一种可能很快浮现出来。最小化意外能为备选假说的选择提供标准。还有一条不那么明显的思路是,如果模型预测与输入数据之间的不匹配(意外)很小,只需利用大脑自由能原理就能简单实现参数的快速调整(通过反馈改变突触强度)。而如果这个快速过程不顺利,输入与模型预测之间的不一致程度一直很高,可能就会触发复杂引擎策略进行范围更广的尝试。后面这个过程很有可能就是当人们在“思考”某件事的时候发生的事情。
有没有复杂引擎在大脑功能中扮演重要角色的证据?
贝叶斯脑假说从统计的角度来研究这个问题,将大脑视为一台统计推断机器。模型参数的概率分布被视为在模型范围内囊括了“所有可能性”。自由能原理提供了内部生成原则,让系统可以“孕育”出最优解。换句话说,它提供了一种在神经元层面上在各种可能性中进行选择的方法。
贝叶斯大脑的思想综合了20年来的几条思路。近年来贡献最多的是伦敦大学学院的Karl Friston。进一步了解可参考3篇综述文章:
“The Bayesian Brain:The Role of Uncertainty in Neural Coding and Computation.”David C.Knill&Alexandre Pouget, TRENDS in Neuroscience 27:712—719(2004);
“The Free Energy Principle.”Karl Friston, Nature Reviews Neuroscience 2:127—138(2010);
“Hierarchical Bayesian Inference in the Visual Cortex.”Tai Sing Lee&David Mumford.J.Opt.Soc.Am A.,20:1434—1448(2003)。
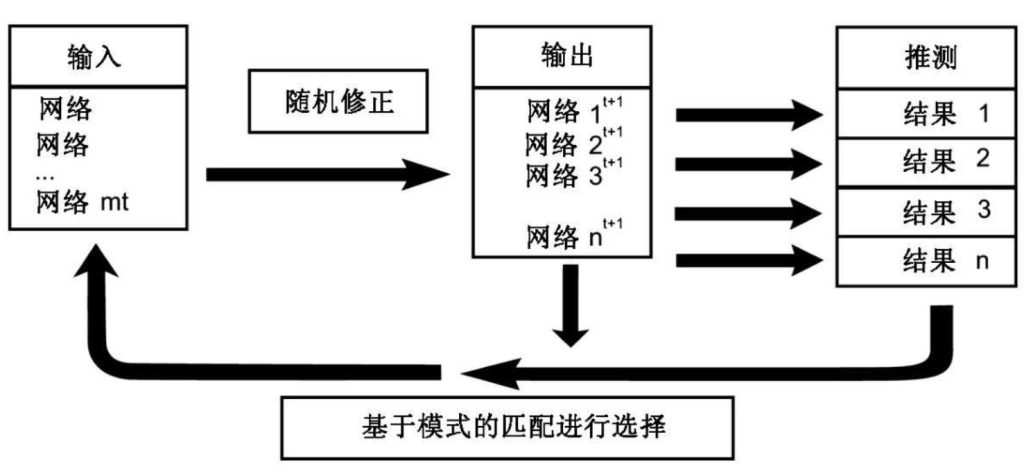
图10.1展示了用大脑领域的词汇重新绘制的复杂引擎。这幅图大致揭示了复杂引擎是如何作用于大脑中累积性的选择网络从而产生有用的结果。这个循环从产生适量的“猜测”开始,即贝叶斯脑框架中针对某个问题的试探性模型(图中的“输出”)。这些猜测以并行的神经通信模式或网络的形式实现。通过将得出的结果与针对的问题进行匹配来检验猜测。匹配最糟糕的(有最大意外的那些)被抛弃。匹配最好的会被随机修正,产生出多个新的输出。然后又再次检验得到的结果。反复的循环很快会使得得到的结果与问题匹配得越来越好。
IPCS循环与强化学习的马尔可夫决策过程非常类似:
《统计学习方法》李航
概率把常识简化为了计算。 ——拉普拉斯
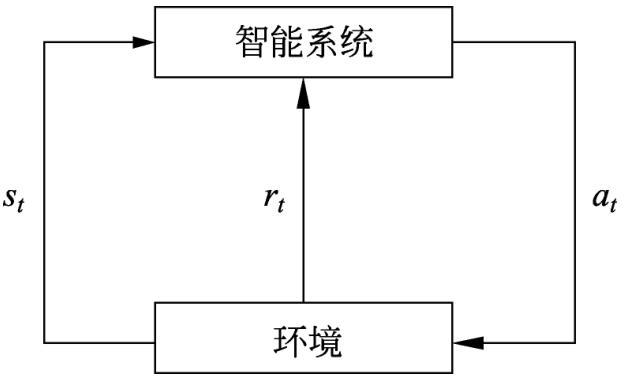
强化学习(reinforcement learning)是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程(Markov decision process),智能系统能观测到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯决策。智能系统与环境的互动如图1.3所示。在每一步t,智能系统从环境中观测到一个状态(state)st与一个奖励(reward)rt,采取一个动作(action)at。环境根据智能系统选择的动作,决定下一步t+1的状态st+1与奖励rt+1。要学习的策略表示为给定的状态下采取的动作。智能系统的目标不是短期奖励的最大化,而是长期累积奖励的最大化。强化学习过程中,系统不断地试错(trial and error),以达到学习最优策略的目的。
强化学习的马尔可夫决策过程是状态、奖励、动作序列上的随机过程,由五元组<S,A,P,r,γ>组成。
· S是有限状态(state)的集合
· A是有限动作(action)的集合
· P是状态转移概率(transition probability)函数:[插图]
· r是奖励函数(reward function):r(s,a)=E(rt+1|st=s,at=a)
· γ是衰减系数(discount factor):γ∈[0,1]